Surface Area of Rectangular Prism – Formula, Facts, Examples

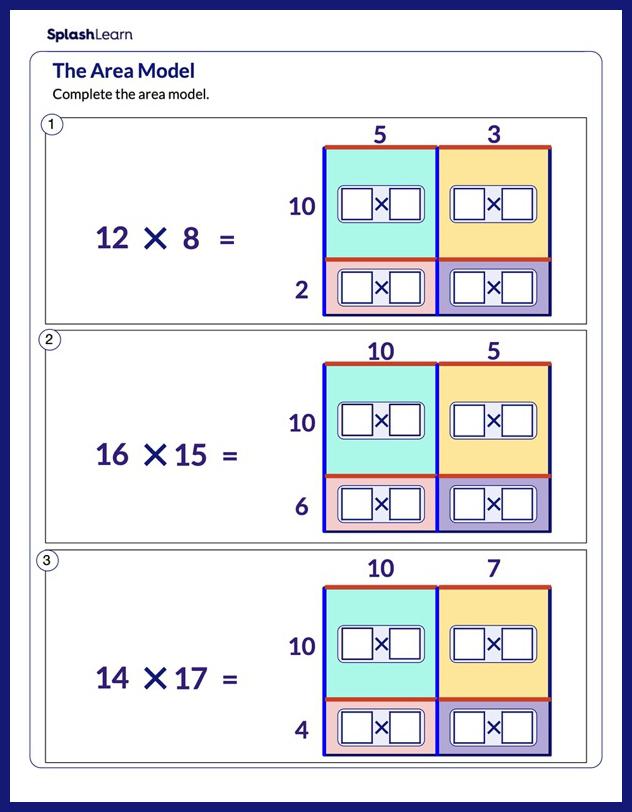
What Is the Surface Area of a Rectangular Prism?

The total surface area of a rectangular prism (cuboid) is the total area covered by the surfaces (lateral and base) of a rectangular prism.

A rectangular prism consists of 6 faces, each of which are rectangles. Its bases are congruent and parallel to each other. A right rectangular prism is also called a cuboid.

Note: Rectangular prisms are of two types: right rectangular prisms and oblique rectangular prisms. Throughout the article, the term ‘rectangular prism’ refers to ‘right rectangular prism.’

The right rectangular prism has two parallel and congruent rectangular faces as its bases and four lateral faces, each one of them a rectangle. Also, the faces are perpendicular to each of its bases. The faces of an oblique rectangular prism are parallelograms. 

We can study the surface area of a rectangular prism as

• Base areas: The area of two rectangles at its base.

• Lateral Surface Area: Lateral Surface Area of a Rectangular Prism is the area of the faces of the prism excluding the area of the base and the top. Suppose you have to paint the walls of the room. In such cases, we will exclude the area of ceiling and flooring. 

• Total Surface Area: Total Surface Area of a rectangular prism is the area of all the faces of the prism including the area of the bases and the LSA.

Surface Area of Rectangular Prism: Formulas

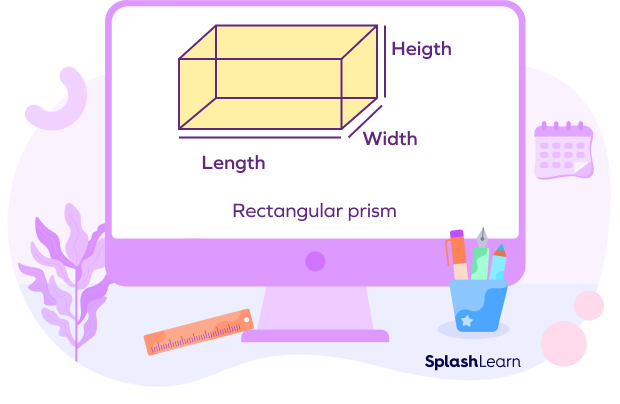
Type of surface area	Description	Formula
Base Area	Area of the base	Area of one base = lw Area of two bases = 2lw
Lateral Surface Area (LSA)	Area of the lateral sides (faces)	LSA = 2h(h + w)
Total Surface Area (TSA)	LSA + Area of two bases	TSA = 2wh + 2lh + 2lw TSA = 2(lw + wh + lh)

Note: Breadth (b) and width (w) are two terms that are commonly used when discussing the measurements. They are often used interchangeably, especially when referring to the dimensions of a rectangular object. 

In this context, both terms describe the measurement of the shorter side that is perpendicular to the length and height. So, we can also define the formulas by replacing w by b. However, there may be subtle differences in the meaning of these terms in other contexts.

Derivation of the Surface Area of Rectangular Prism Formula

Assume that l, w, h are the length, width, and height of the rectangular prism respectively.

A rectangular box has 6 sides (faces): top/bottom, front/back, left side and right side. 

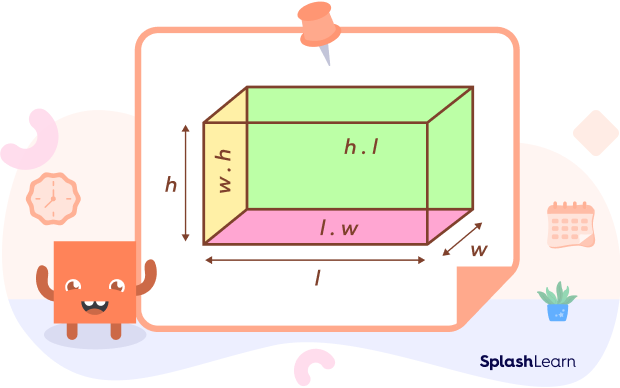
There are two faces (front and back) with dimension l ✕ h.

Area of these two faces = 2(l ✕ h)

There are two faces (top and bottom ones) with dimension l ✕ w.

Area of these two faces = 2(l ✕ w)

There are two faces (left and right) with dimension w ✕ h.

Area of these two faces = 2(w ✕ h)

The Lateral Surface Area is the sum of the faces of a rectangular prism except the top and base. 

Lateral surface area of rectangular prism = lh + wh + lh + wh

LSA =2lh + 2wh

LSA = 2h(l + w)

The total surface area is the sum of all the faces of a rectangular prism.

Total Surface Area of rectangular prism = 2lw + 2wh + 2hl  

TSA = 2(lw + wh + hl)

How to Find the Surface Area of a Rectangular Prism

Step 1: Check if the dimensions of the rectangular prism are in the same units or not. If not, convert them into the same units.

Step 2: Once the dimensions are of the same units, understand whether you have to calculate the lateral surface area or the total surface area according to the given situation. 

Step 3: Apply the formulas: 

 lateral surface area = 2h(l + w)

 total surface area = 2(lw + wh + lh) 

Example: Jasmine has to wrap a rectangular box of length 20 in, breadth 10 in and height 7 in. How much wrapping paper does she need? 

Rectangular box simply means rectangular prism or cuboid. To wrap a rectangular box, Jasmine needs to cover the entire surface of the box.

So, we need to find the TSA.

Here l = 20 m, w = 10 m and h = 7 m

TSA = 2(lw + wh + hl)

TSA  = 2 (20 ✕ 10 + 10 ✕ 7 + 20 ✕ 7) 

TSA = 2(200 + 70 + 140) 

TSA = 2 ✕ 410 

TSA = 820 square inches

 So, Jasmine needs 820 square inches of wrapping paper. 

Facts about Surface Area of Rectangular Prism

Solved Examples on Surface Area of Rectangular Prism

1. What is the lateral surface area of a rectangular prism with length 10 m, breadth 8 m and height 2 m?

Solution: 

l = 10 m, w = 8 m, h = 2 m

Lateral Surface Area = 2h(l + w) 

Lateral Surface Area = 2 ✕ 2 (10 + 8)

Lateral Surface Area = 4 ✕ 18 

Lateral Surface Area  = 72 square meter

2. What is the total surface area of a rectangular prism with length 42 inches, breadth 30 inches and height 15 inches?

Solution: 

l = 42 in, b = 30 in, h = 15 in

Total Surface Area = 2(lb + bh + hl) 

Total Surface Area = 2(42 ✕ 30 + 30 ✕ 15 + 15 ✕ 42) 

Total Surface Area = 2(1260 + 450 + 630) 

Total Surface Area = 2 ✕ 2340 

Total Surface Area = 4680 square inches.

3. A fish tank has the shape of a rectangular prism with length (l) = 8 in, Breadth (b) = 5 in and Height (h) = 5 in. What will be the total surface area of the fish tank?

Solution: 

l = 8 in, b = 5 in, h = 5 in

T.S.A = 2(8 ✕ 5 + 5 ✕ 5 + 5 ✕ 8) 

T.S.A = 2(40 + 25 + 40) 

T.S.A = 2 ✕ 105 

T.S.A = 210 square inches

4. Emily built a rectangular box with an open top. The box is 12 inches long, 5 inches wide, and 9 inches high. How much cardboard should she buy?

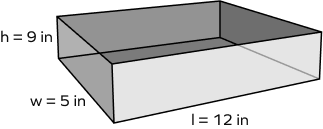
Solution: 

The box has an open top. So, we will not consider the area of the top face.

l = 12 inches, b = 5 inches, h = 9 inches

Surface Area = lw + 2hl + 2hw 

Surface Area = lw + 2h(l + w)

Surface Area = (12 ✕ 5) + 2 ✕ 9 ✕ (12 + 5) 

Surface Area = 60 + 306 

Surface Area = 366 square inches

5. The total surface area of a rectangular prism is 96 ft2 with a base area of 12 ft2 and the perimeter of the base being 18 ft. Determine its height of the rectangular prism.

Solution: 

Base Area = Top Area = lb = 12 ft²

Perimeter = 2(l + b) = 18 ft

T.S.A = 96 ft²

2lb + 2h(l + b) = 96

2 ✕ 12 + 18 ✕ h = 96

24 + 18h = 96

18 h = 72

h = 4 ft

Practice Problems on Surface Area of Rectangular Prism

Frequently Asked Questions on the Surface Area of Rectangular Prism?