- What Is the Triangle Proportionality Theorem?
- Proof of the Triangle Proportionality Theorem
- Converse of the Triangle Proportionality Theorem
- Solved Examples on Triangle Proportionality Theorem
- Practice Problems on Triangle Proportionality Theorem
- Frequently Asked Questions on Triangle Proportionality Theorem
What Is the Triangle Proportionality Theorem?
Triangle proportionality theorem is also known as “basic proportionality theorem” or “Thales theorem,” or “side-splitter theorem.” It was proposed by a famous Greek mathematician Thales.
The theorem is helpful in understanding the concept of similar triangles.
The triangle proportionality theorem uses a line drawn parallel to one side of a triangle to determine the proportions of the other two sides.
If you draw a line parallel to any one side of a triangle that intersects the other two sides of the triangle in two distinct points, then the line divides the other two sides in the same ratio.
y.
Recommended Games
Triangle Proportionality Theorem: Statement
The triangle proportionality theorem states that if a line parallel to one side of a triangle intersects the other two sides at different points, then it divides the remaining two sides proportionally.
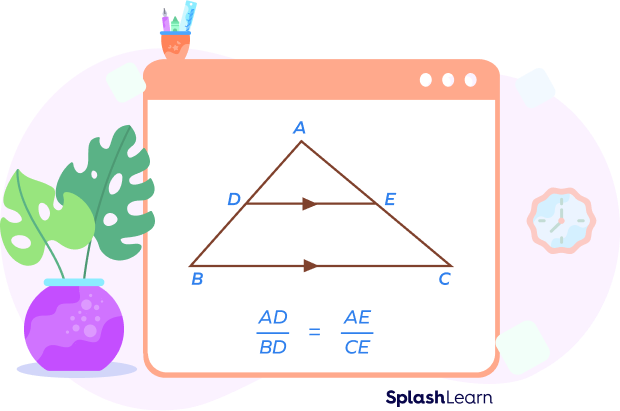
Here, the line DE is parallel to the side BC. It intersects sides AB and AC at two distinct points, D and E.
According to the triangle proportionality theorem, a ratio of AD to DB is equal to the ratio of CE to AE.
Hence, $\frac{AD}{BD} = \frac{AE}{CE}$
Recommended Worksheets
Proof of the Triangle Proportionality Theorem
Given: In $\Delta ABC$, the line segment DE is drawn parallel to the side BC.
To prove: $\frac{AD}{BD} = \frac{AE}{CE}$
Construction: Join the vertex B to the point E. Join the vertex C to the point D.
Draw $EG\; \bot \;AB$ and $DF\; \bot \;AC$ as shown in the given figure.
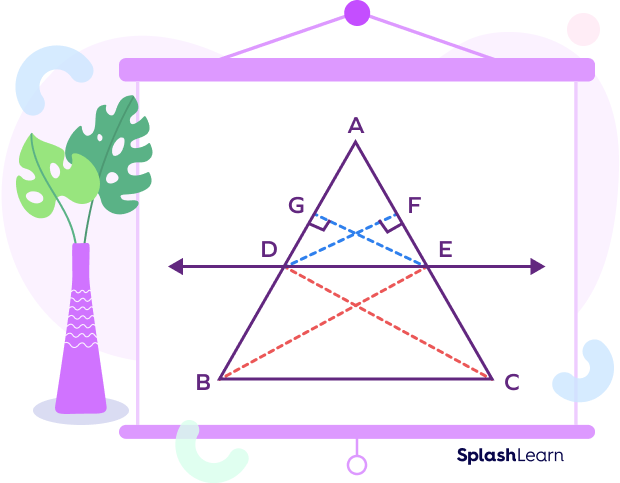
In $\Delta ADE$ and $\Delta BDE$,
$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta BDE)} = \frac{\frac{1}{2} \times AD \times EG}{\frac{1}{2} \times BD \times EG}$ (Both the triangles have the same height EG.)
$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta BDE)} = \frac{AD}{BD}$ …(1)
Now In $\Delta CDE$ and $\Delta ADE$,
$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta CDE)} = \frac{\frac{1}{2} \times AE \times DF}{\frac{1}{2} \times CE \times DF}$ (Both the triangles have the same height DF.)
$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta CDE)} = \frac{AE}{CE}$ …(2)
$\Delta BDE$ and $\Delta CDE$ are lying between the same parallel lines DE and BC.
Triangles having the same base and lying between the same parallels are equal in area.
$\therefore\; Area\; of\; \Delta BDE = Area\; of\; \Delta CDE$
Using this result in equation (1) and (2), we get left sides equal.
$\frac{(Area\; of\; ADE)} {(Area\; of\; BDE)} = \frac{(Area\; of\; ADE)} {(Area\; of\; CDE)}$
Thus, from equation (1) and (2), we get
$\frac{AD}{BD} = \frac{AE}{CE}$
Hence, proved.
Converse of the Triangle Proportionality Theorem
If a line segment divides any two sides of a triangle proportionally (in the same ratio), then the line is parallel to the third side of the triangle.
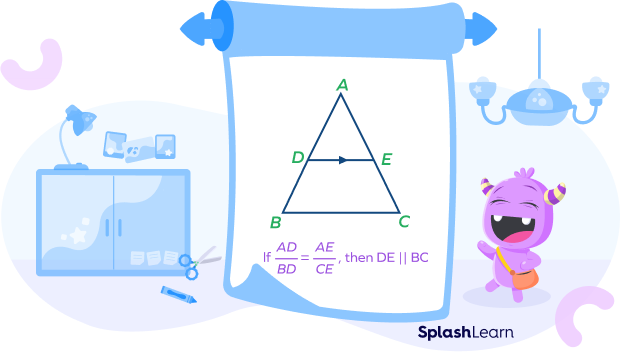
Here, if the line segment DE divides sides AB and AC in equal proportion, i.e., $\frac{AD}{BD} = \frac{AE}{CE}$, then
by the converse of the triangle proportionality theorem, we can say that the line DE must be parallel to BC or $DE\; || \;BC$.
Proof of the Converse of the Triangle Proportionality Theorem
Given: In ΔABC, the line segment DE divides the sides AB and AC in equal proportion. ADBD=AECE.
To prove: DE || BC
Construction: Let us assume DE is not parallel to BC. So draw another line DF, which is parallel to BC.
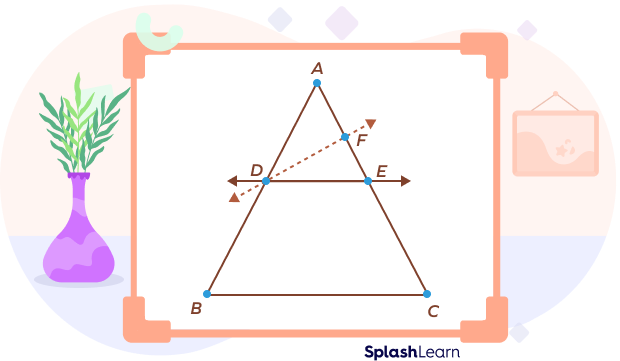
Proof:
Now, we have to show that points E and F are identical or that DE and DF represent the same lines.
According to the Basic Proportionality theorem,
$\frac{AD}{BD} = \frac{AF}{CF}$ … (1)
Also, $\frac{AD}{BD} = \frac{AE}{CE}$ (given) … (2)
From equation (1) and (2), we get
$\frac{AF}{CF} = \frac{AE}{CE}$
Adding 1 on both sides, we get
$\frac{AF}{CF} + 1 = \frac{AE}{CE} + 1$
$\frac{AF + CF}{CF} = \frac{AE + CE}{CE}$
$\frac{AC}{CF} = \frac{AC}{CE}$
$\therefore\; CF = CE$
Therefore, from the above statement, we can conclude that the points E and F are the same points. So, DE and DF represent the same lines.
Hence, $DE\; || \;BC$.
Thus, it proves the converse of the basic proportionality theorem.
Facts about Triangle Proportionality Theorem
- The well-known Greek mathematician Thales proposed the basic proportionality theorem, which is why it is also known as the Thales theorem.
- In daily life, the triangle proportionality theorem has applications in the construction of houses, bridges, towers, etc.
Conclusion
In this article, we have learned about the triangle proportionality and converse of triangle proportionality theorem with statement, proof, applications, facts. Let’s solve a few examples.
Solved Examples on Triangle Proportionality Theorem
- In the figure given below ST || QR, find the ratio PT : TR.
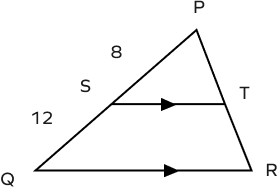
Solution:
$PS = 8,\; SQ = 12$
$ST\; || \;QR$
According to the triangle proportionality theorem, the ratio of PS to SQ is equal to the ratio of PT to TR.
$\frac{PS}{SQ} = \frac{PT}{TR}$
$\frac{8}{12} = \frac{PT}{TR}$
$\Rightarrow \frac{2}{3} = \frac{PT}{TR}$
$\Rightarrow PT\;:\;TR =2\;:\;3$
- Check whether the line PQ is parallel to the BC or not.
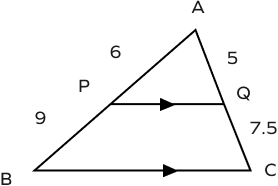
Solution:
$AP = 6,\; BP = 9,\; AQ = 5,$ and $CQ = 7.5$
$\frac{AP}{BP} = \frac{6}{9} = \frac{2}{3}$
$\frac{AQ}{CQ} = \frac{5}{7.5} = \frac{2}{3}$
Since, $\frac{AP}{BP} = \frac{AQ}{CQ}$
Hence, by the converse of triangle proportionality theorem, the line PQ is parallel to the BC.
- In the figure given below $DE\; || \;BC$, find the value of “x.”
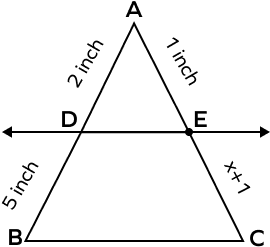
Solution:
Given, $DE\; || \;BC,\; AD = 2$ in, $BD = 5$ in, $AE = 1$ in, and $CE = x + 1$
According to the triangle proportionality theorem,
$\frac{AD}{BD} = \frac{AE}{CE}$
$\Rightarrow \frac{2}{5} = \frac{1}{x + 1}$
$\Rightarrow 2x + 2 = 5$
$\Rightarrow 2x = 3$
$\Rightarrow x = \frac{3}{2} = 1.5$ in
Hence, the value of x is 1.5 inches.
- In the figure given below, $PQ\; || \;BC$, find the value of x.
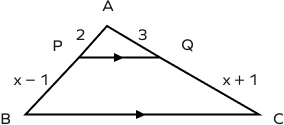
Solution:
Given, $PQ\; || \;BC,\; AP = 2,\; BP = x \;−\; 1,\; AQ = 3,$ and $CQ = x + 1$
According to the triangle proportionality theorem,
$\frac{AP}{BP} = \frac{AQ}{CQ}$
$\Rightarrow \frac{2}{x \;-\;1} = \frac{3}{x\;+\;1}$
$\Rightarrow 2(x\;+\;1) = 3(x\;-\;1)$
$\Rightarrow 2x\;+\;2 = 3x\;-\;3$
$3x\;-\;2x = 3+2$
$x = 5$
Hence, the value of x is 5.
Practice Problems on Triangle Proportionality Theorem
Triangle Proportionality Theorem: Statement, Proof, Examples
In the figure below $DE\; || \;BC$. By the triangle proportionality theorem, we can write $\frac{AE}{EC}=$ ?
From the given figure, $\frac{AD}{BD} = \frac{2}{3} = 2\; : \;3$.
For $DE\; || \;BC$, the values of AE and CE must be in the same ratio as $AD\;: \;BD$
$AE\; : \;CE = 4\; : \;6 = 2\; : \;3$..

Which of the following is correct for the figure below?
From the given figure, $AE\; : \;CE = 2\;: \;4 = 1\;: \;2,\; AD\;: \;BD = 1\;:\;2$
Since, $\frac{AD}{BD} = \frac{AE}{CE}$, hence, according to the converse of triangle proportionality theorem $DE\; || \;BC$.
Therefore, all of the above i.e. option (d) is correct.

Which of the following is the triangle proportionality theorem’s condition such that the equation $\frac{AP}{PB} = \frac{AQ}{QC}$ becomes true?
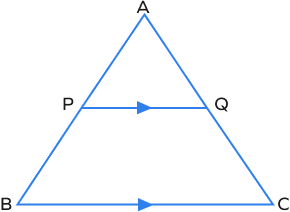
If a line parallel to one side of a triangle intersects the other two sides at different points, then it divides the two sides proportionally.
Thus, if $PQ\; || \;BC$, we have $\frac{AP}{PB} = \frac{AQ}{QC}$.
Frequently Asked Questions on Triangle Proportionality Theorem
What are the uses of the triangle proportionality theorem?
In daily life, it is used in the construction of houses, bridges, towers, etc., where precision and proportions are important.
What is the other name of the triangle proportionality theorem?
The triangle proportionality theorem is also known as the Thales theorem or basic proportionality theorem.
What is the formula of the triangle proportionality theorem?
In any $\Delta ABC$ where line segment DE is drawn parallel to the side BC of $\Delta ABC,\; \frac{AD}{BD} = \frac{AE}{CE}$.
What is the converse of the triangle proportionality theorem?
If a line segment divides any two sides of a triangle in equal proportion, then the line is parallel to the third side of the triangle.
What is the basic proportionality theorem?
The basic proportionality theorem (B.P.T.) states that if a line is drawn parallel to one side of a triangle and is cutting the other two sides, then it divides the other two sides in equal proportion.
It is also known as the Thales theorem.



























