What Is y $=$ mx $+$ b?
The equation of line can be written in different forms: two-point form, slope-intercept form, standard form. So, what does slope intercept form look like?
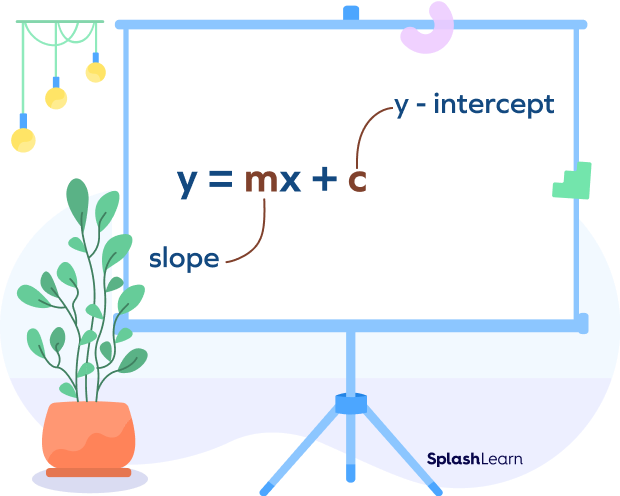
The equation y $= mx + b$ represents the slope-intercept form of a straight line.
It is the most simple since it is based on just two values and requires no complex calculations.
Let’s understand the meaning of $y = mx + b$.
- x and y
x and y are coordinates of any two points on the line. So, x and y are variables.
- What is m?
m in $y = mx + b$ represents the slope of the line. It tells us how steep the line is.
- What is b in $y = mx + b$?
It’s the y-intercept of the line. It’s the point at which the line intersects the y-axis.
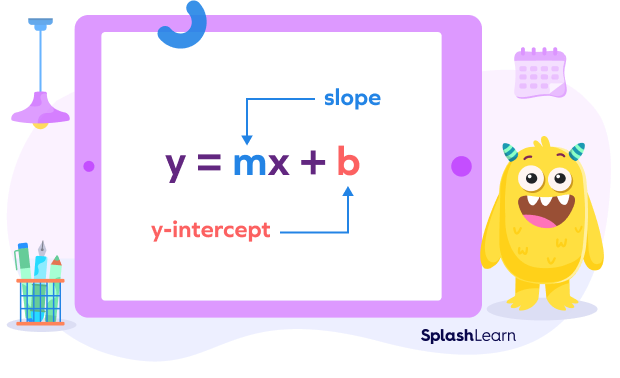
Note: Sometimes the y-intercept is also represented using the letter “c” and in that case, the equation of line becomes $y = mx + c$.
Example: Find the equation of a line having slope 3 and y-intercept 2.
Here, $m = 3$ and $b = 2$
Equation of line using the slope-intercept form is $y = mx + b$.
Required equation of the line: $y = 3x + 2$
Recommended Games
How to Find y $=$ mx $+$ b
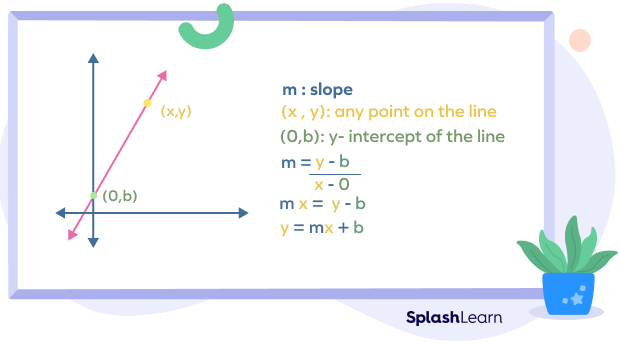
Let’s derive the slope-intercept form. Consider a line whose y-intercept is b. In simple words, the line passes through the point (0,b). Let (x,y) be the coordinates of any point on the line.
Now, we have coordinates of two points on the line: (x,y) and (0,b).
Let the slope of the given line be m.
The formula to find the slope of the straight line is
$m = \frac{change\; in\; y}{change\; in\; x} = \frac{Difference\; in\; y\;-\;coordinates}{Difference\; in\; x\;-\;coordinates}$
So, if the points $(x_1,\;y_1)$ and $(x_2,\;y_2)$ lie on the given line.
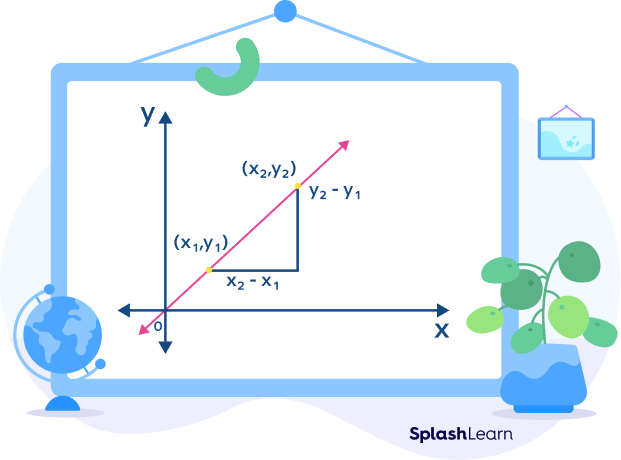
We can find the slope as
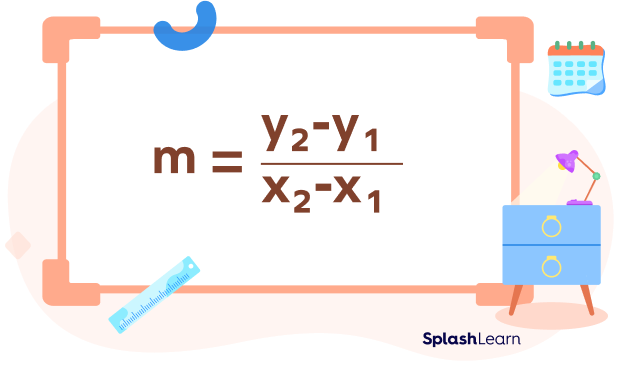
Thus, in our case
$\Rightarrow m = \frac{y \;-\; b}{x \;-\; 0}$
$\Rightarrow m = \frac{y \;-\; b}{x}$
$\Rightarrow mx = y\;-\;b$
$\Rightarrow y = mx + b$
Recommended Worksheets
y $=$ mx $+$ b at Origin
Let’s understand how to solve $y = mx + b$ at origin. The equation of a straight line with slope “m” passing through the origin (0,0) is given as:
$y = \frac{y \;-\; 0}{x \;-\; 0}$
$y = mx$
So, for any line passing through origin, the y-intercept is 0.
Writing an Equation in the Slope Intercept Form
In this section, we will learn to write an equation in the slope intercept form.
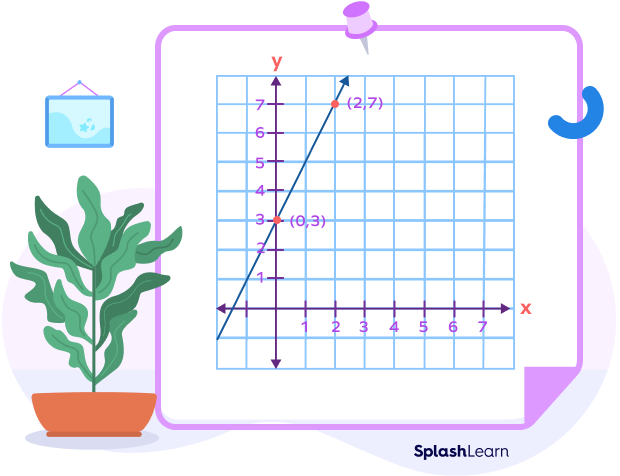
Example: Let’s write the equation of the line that passes through the points (0,3) and (2,7) in slope-intercept form.
Here, $x_1 = 0,\;y_1 = 3,\;X_2 = 2,\; , y_2 = 7$
The slope-intercept form is $y = mx + b$.
The line passes through the point (0, 3). Thus, the y- intercept of the line is 3.
So, $b = 3$.
The slope is calculated as
$m = \frac{y_2 \;-\; y_1}{x_2 \;-\; x_1}$
$m = \frac{7 \;-\; 3}{2 \;-\; 0}$
$m = \frac{4}{2}$
$m = 2$
Putting these values in the standard equation, we get-
$y = 2x + 3$
Facts about y $=$ mx $+$ b
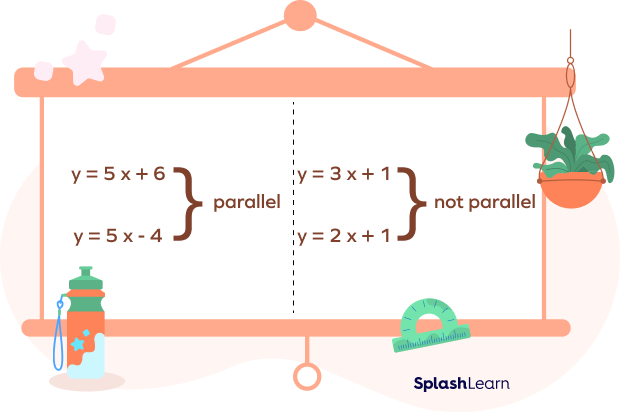
Slopes of two parallel lines are always equal. So, we can identify two parallel lines using their equations in the slope-intercept form.
The product of the slopes of two mutually perpendicular lines equals to $-1$. So, we can identify two perpendicular lines using their equations in the slope-intercept form.Example: The lines $y = \frac{5}{6} x + 2$ and $y = \frac{-6}{5} x + 2$ are perpendicular since the product of the slopes is $\frac{5}{6} \times \frac{-6}{5} = \;-\;1$
Conclusion
In this article, we learnt about slope intercept form $y = mx + b$, the formula to find the slope, and writing the equation of a line using slope-intercept form. Let’s solve a few examples!
Solved Examples on y $=$ mx $+$ b
1. Find the slope of the line joining the points P$(0,\; –\;1)$ and Q$(4,\;1)$.
Solution:
The two points on the line are P$(0,\; –2)$ and Q$(4,\; 1)$.
We know that, the slope of line passing through the points $(x_1,\;x_1)$ and $(x_2,\; y_2)$ is given by
$m = \frac{y_2 \;-\; y_1}{x_2 \;-\; x_1}$
$m = \frac{\;-\;2 \;-\; 1}{0 \;-\; 4}$
$m = \frac{\;-3}{-\;4}$
$m = \frac{3}{4}$
2. Find the equation of line passing through points P$(–\;2,\; 5)$ and Q$(0,\; –\;3)$ and having y-intercept 3.
Solution:
P$(–\;2,\; 5)$ and Q$(0,\; –\;3)$ are the two points on the line. Therefore, slope of the line is given by
$m = \frac{5 \;-\; ( \;-\; 3)}{ \;-\; 2 \;-\; 0} = \frac{8}{\;-\;2} = \;-\;4$
y-intercept $= 3$
Thus, the equation of line is $y = \;-\;4x + 3$.
3. What is the slope of the line: $y = \;−\;5x + 17$?.
Solution:
If we compare the given equation with $y = mx + b$, where m is the slope and b is the y-intercept, then we get,
A slope of the line whose equation is $y = \;-\;5x + 17$ is $\;-\;2$.
$m = \;-\;5$
4. If the slope of a straight line is 3 and y-intercept is 4, then find the equation of the line.
Solution:
We know that the equation of line in slope-intercept form is given by:
$y = mx + b$
Given, $m = 3$ and $b = 4$, thus, the required equation is:
$y = 3x + 4$
5. What is the slope and y-intercept of the equation $y = 2x$?
Solution:
If we compare the given equation with $y = mx + b$, where m is the slope and b is the y-intercept, we get
Slope $= m = 2$ and y-intercept $= b = 0
Practice Problems on y $=$ mx $+$ b
y $=$ mx $+$ b – Definition, Slope Intercept Form, Examples, Facts
What is the slope of the line $y = 2x +3$?
Comparing the equation of the line with the slope-intercept form $y = mx + b$, we get slope $= m = 2$.
What is the slope of a line joining two points $(4,\; 8)$ and $(\;-\;7,\; 1)$?
The slope of line joining two points $(4,\; 8)$ and $(\;-\;7,\; 1)$ is calculated by
$m = \frac{1 \;-\; 8}{\;-\; 4 \;-\;7} = \frac{\;-\;7}{\;-\;11} = \frac{7}{11}$
What is the slope of the line: $3y = 2x + 9$?
Given equation of line is $3y = 2x + 9$.
$y = \frac{2}{3} x + 3$
Comparing with $y = mx + b$, we get
slope $= m = \frac{2}{3}$
What is the slope-intercept form of a line with slope 3 and y-intercept -2?
The slope-intercept form of a line is $y = mx + b$.
Thus, the equation of line is $y = 3x -2$.
The lines $y = 2x + 1$ and $y = 2x\;-\;1$ are
The slopes of two parallel lines are equal. The slopes of $y = 2x + 1$ and $y = 2x\;-\;1$ is 2. So, they are parallel.
Frequently Asked Questions on y $=$ mx $+$ b
What is the equation of x-axis and y-axis?
Equation of x-axis is $y = 0$ and the equation of y-axis is $x = 0$.
How to convert a standard form of straight line equation into the slope-intercept form?
The standard form of the equation of a straight line is given as:
$Ax + By + C = 0$.
Rearranging this standard form, you can find the slope intercept of any straight line given in this form as,
$y = (\frac{\;-\;A}{B})x + (\frac{\;-\;C}{B})$, where, $\frac{\;-\;A}{B}$ represents the slope of the line and $(\frac{\;-\;C}{B})$ is the y-intercept.
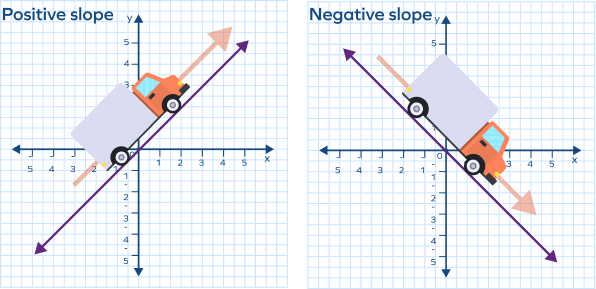
What is a positive or negative slope?
A positive slope means y increases as x increases.
Visually, the line moves up as we go from left to right.
A negative slope means y decreases as x increases
Visually, the line moves down as we go from left to right.
What is a 0 slope?
A zero slope means that y is constant and it does not change as x changes. So, the equation of line having 0 slope is $y = c$, where c is constant. It is basically a horizontal line.